[번역] 자바스크립트 메모이제이션

scotch 의 Philip Obosi 이 작성한 Understanding Memoization In JavaScript 번역 자료입니다. 번역에 문제가 있다면 댓글 달아주시구요. 원문을 보시기를 추천드립니다

목차

• 메모이제이션이 무엇인가요?
• 메모이제이션이 중요한 이유는 무엇인가요?
• 메모이제이션은 어떻게 동작하나요?
• 케이스 스터디: 피보나치 수열
• JSPerf로 성능 테스트
• 함수형 접근
• memoizer 함수 테스트
• 함수를 메모화(memoize) 할 때
• 메모이제이션 라이브러리
• 결론
• 추가 읽기

애플리케이션이 증가하고 더 많은 양의 컴퓨팅을 수행하기 시작하면서 속도(🏎)에 대한 요구도 증가하고 프로세스 최적화도 필수 요소가 되었습니다. 이 문제를 무시하면 실행 중에 많은 시간이 걸리고 엄청난 양의 시스템 리소스를 소모하는 프로그램이 됩니다.

메모이제이션(Memoization)은 비용이 많이 드는 함수 호출의 결과를 저장하고 동일한 입력이 다시 발생할 때 캐시된 결과를 반환하여 애플리케이션 속도를 높이는 최적화 기술입니다. 아직 이 말이 이해가 되지 않더라도 괜찮습니다. 이 포스트는 메모이제이션이 필요한 이유, 그것이 무엇인지, 어떻게 구현할 수 있고 언제 사용해야하는지에 대한 심도있는 설명을 제공합니다.

메모이제이션이 무엇인가요?

메모이제이션은 비싼 함수 호출(expensive function calls) 결과를 저장하고 동일한 입력이 다시 제공될 때 캐시된 결과를 반환하여 응용 프로그램의 속도를 높이는 최적화 기술입니다.

같은 정의? 🙈 이번에는 좀 더 자세히 살펴보겠습니다.

이 시점에서 메모이제이션의 목적은 "비싼 함수 호출(expensive function calls)"을 실행하는데 소비되는 시간과 자원의 양을 줄이는 것입니다.

비싼 함수 호출은 무엇입니까?

혼동하지 마세요. 여기서 돈을 쓰지는 않습니다. 컴퓨터 프로그램의 관점에서 우리가 가진 두 가지 주요 자원은 시간과 메모리입니다. 그러므로 비싼 함수 호출은 무거운 계산 실행 중에 이 두 리소스의 큰 덩어리(chunks)를 소비하는 함수 호출입니다.

돈과 마찬가지로, 우리는 경제적이 될 필요가 있습니다. 이를 위해, 메모이제이션은 캐싱을 사용하여 나중에 빠르고 쉽게 액세스할 수 있도록 함수 호출의 결과를 저장합니다.

캐시는 해당 데이터에 대한 향후 요청이 더 빠르게 처리될 수 있도록 데이터를 보관하는 임시 데이터 저장소입니다.

따라서 비용이 비싼 함수가 한 번 호출되면 결과가 캐시에 저장되어 애플리케이션 내에서 함수가 다시 호출 될 때마다 계산을 다시 실행하지 않고 캐시에서 결과가 매우 빠르게 반환됩니다.

메모이제이션이 중요한 이유는 무엇인가요?

메모이제이션의 중요성을 보여주는 예제입니다:

공원에서 매력적인 표지의 새 소설을 읽고 있다고 상상해보세요. 사람이 지나갈 때마다 표지에 그려진 커버 때문에 책의 이름과 책의 저자를 묻습니다. 첫 번째 질문이 나올 때 표지를 뒤집고 저자의 제목과 이름을 읽습니다. 이제 점점 더 많은 사람들이 같은 질문을 합니다. 당신은 매우 좋은 사람🙂 이므로 모든 질문에 답합니다.

표지를 뒤집어 제목과 저자의 이름을 각각에게 읽어 주실 건가요? 기억에서 응답을 하시겠어요? 어떤 것이 더 시간이 절약되나요?

비슷한 점이 보이시나요? 메모이제이션과 함께 함수가 입력을 제공할때 필요한 계산을 수행하고 값을 반환히기 전에 결과를 캐시에 저장합니다. 같은 입력을 나중에 받게 된다면 반복할 필요가 없습니다. 캐시(메모리)에서 응답을 제공하기만 하면됩니다.

아주 간단 하죠? 이제 어떻게 작동하는지 알고 싶습니까? 보시죠!

메모이제이션은 어떻게 동작하나요?

자바스크립트의 메모이제이션 컨셉은 주로 두가지 개념으로 만들어집니다:

• 클로저(Closure)
• 고차함수(Hiher Order Functions)(함수에서 함수반환)

클로저

클로저는 함수의 해당 함수가 선언된 어휘 환경(lexical environment)의 결합이다.

명확하지 않습니까? 저도 그렇게 생각합니다.

좀더 명확하게 이해하기 위해 자바스크립트에서 어휘 스코프(lexical scope)의 개념을 빠르게 살펴보겠습니다. 어희 스코프는 단순히 코드를 작성하는 동안 프로그래머가 지정한 변수와 블록의 물리적 위치를 가리킵니다.

Kyle Simpson의 책 ”You Don’t Know JS”에서 채택한 매우 인기있는 코드 스니펫을 보세요. :

function foo(a) {
  var b = a + 2;
  function bar(c) {
    console.log(a, b, c);
  }
  bar(b * 2);
}

foo(3); // 3, 5, 10

이 코드 스니펫에서 3개의 범위(scope)를 확인할 수 있습니다:

• 글로벌 스코프(유일한 식별자로 foo를 포함)
• 식별자 a, b 및 bar가 있는 foo 스코프
• 식별자 c를 포함하는 bar 스코프

위의 코드를 자세히 보면 foo 내부에 내포되어 있는 bar 함수가 변수 a와 b에 접근할 수 있다는 것을 알 수 있습니다. 함수 bar를 환경(environment)과 함께 저장하는 것을 주목합시다. 따라서 우리는 bar가 foo의 범위에 폐쇄(closure)되어 있다고 말합니다.

여러분은 유전의 관점에서 이것을 이해할지도 모릅니다. 개인이 가까운 환경 밖에서 유전된 특징들에 접근하고 보여줄 수 있다는 것 말입니다. 이 논리는 클로저에 대한 또 다른 요소를 강조하며, 이는 두 번째 주요 개념으로 이어집니다.

함수에서 함수 반환

다른 함수에서 작동하는 함수를 인수로 사용하거나 반환하여 고차 함수(higher-order functions)라고 합니다.

클로저를 사용하면 둘러싼 함수의 어휘 범위 (즉, 둘러싼 함수의 함수의 식별자)에 대한 액세스를 유지하면서 둘러싸는 함수 외부에서 내부 함수를 호출 할 수 있습니다.

이를 설명하기 위해 이전 예제의 코드를 약간 조정해 보겠습니다.

function foo(){
  var a = 2;

  function bar() {
    console.log(a);
  }
  return bar;
}
var baz = foo();
baz();//2

아아아 !!! 흥미롭지 않나요?

함수 foo가 다른 함수 bar를 반환하는 방법에 주목하십시오. 함수 foo를 실행하고 반환된 값을 baz에 할당하는 것을 보세요. 그러나 이 경우에는 반환 함수가 있습니다. 따라서 baz는 이제 foo 내부에 정의된 bar 함수에 대한 참조를 가집니다.

여기서 가장 흥미로운 점은 foo의 어휘 범위 밖에서 함수 baz를 실행해도 콘솔에 기록되는 2의 값을 여전히 얻을 수 있다는 것입니다. 어떻게 가능한 걸까요? 😕

bar는 foo의 범위 밖에서 실행 되더라도 (멀리 떨어져있는 경우에도) 항상 foo (상속 된 특성)의 변수에 액세스 할 수 있습니다.

이제 더 많은 코드 샘플을 사용하여 메모이제이션이 이런 개념을 어떻게 활용하는지 살펴 보겠습니다. 💪🏾

케이스 스터디: 피보나치 수열

피보나치 수열이란 무엇입니까?

피보나치 수열은 1 또는 0으로 시작하고 그 다음에 1로 시작하는 숫자의 집합이며, 각 숫자(피보나치 수라고 함)가 앞의 두 숫자의 합과 같다는 규칙에 따라 계속됩니다. 예를 들면

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

또는

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

과제 : 피보나치 수열에서 ** n 번째 ** 요소를 반환하는 함수를 작성하세요. 수열은 다음과 같습니다.

[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …]

각 값이 이전 두 값의 합계임을 알면 이 문제에 대한 재귀 솔루션은 다음과 같습니다.

function fibonacci(n) {
    if (n <= 1) {
        return 1
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

간결하고 정확합니다! 하지만 문제가 있습니다. 종료 케이스에 도달할 때까지 문제의 크기(n값)를 지속적으로 줄이면 시퀀스에서 특정 값에 대한 반복적인 평가가 있기 때문에 더 많은 작업이 수행되고 솔루션에 도달하는데 시간이 소비됩니다.

아래 다이어그램을 살펴보면 fib(5)을 평가하려고 할 때 다른 분기(branch)에 대한 지수 0, 1, 2 와 3에서 피보나치 수를 반복적으로 찾으려고 노력합니다. 이는 **중복 연산(redundant computation)**이라고 알려져 있으며 메모이제이션으로 제거해야 할 바로 그것입니다.

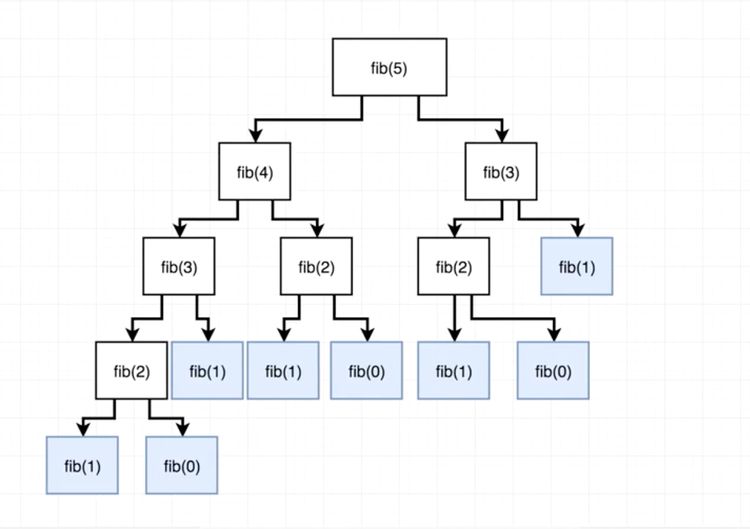
메모이제이션으로 이 문제를 해결하겠습니다.

function fibonacci(n,memo) {
    memo = memo || {}
    if (memo[n]) {
        return memo[n]
    }
    if (n <= 1) {
        return 1
    }
    return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
}

위의 코드 스니펫에서는 memo 라는 선택적 매개 변수를 허용하도록 함수를 조정합니다. 우리는 memo 오브젝트를 캐시로 사용하여 각각의 인덱스와 함께 피보나치 번호를 저장하며 나중에 실행 과정에서 필요할 때마다 검색해야 한다.

memo = memo || {}

여기서는 함수를 호출할 때 memo가 인수로 수신되었는지 확인합니다. 인수가 있다면 사용을 위해 초기화하지만 그렇지 않다면 빈 오브젝트로 설정합니다.

if (memo[n]) {
      return memo[n]
}

그런 다음 현재 키 n에 대해 캐시된 값이 있는지 확인하고 캐시된 값이 있으면 값을 반환합니다.

이전 솔루션과 마찬가지로 n이 1보다 작거나 같은 경우 종료 케이스를 지정합니다.

마지막에는 계산 중에 사용하기 위해 캐시된 값(memo)을 각 함수에 전달하면서 n보다 작은 값을 가진 함수를 재귀적으로 호출한다. 이전에 값을 평가하고 캐시하면 이런 비싼 계산을 두 번 다시 수행하지 않습니다. 캐시 memo에서 값을 검색하기만 하면 됩니다.

최종 결과를 반환하기 전에 캐시에 추가합니다.

휴!!! 지금까지의 수고를 축하합시다! 🙂

우리가 얼마나 더 잘 만들었는지 보시죠!

JSPerf로 성능 테스트

이 링크를 따라 JSperf의 성능 테스트를 수행합니다. (역주: 사이트가 사라졌습니다. ‼️) 여기서는 두 가지 방법을 모두 사용하여 fibonacci(20)를 실행하는데 걸리는 시간을 평가하는 테스트를 실행합니다. 아래 결과를 참조하십시오.

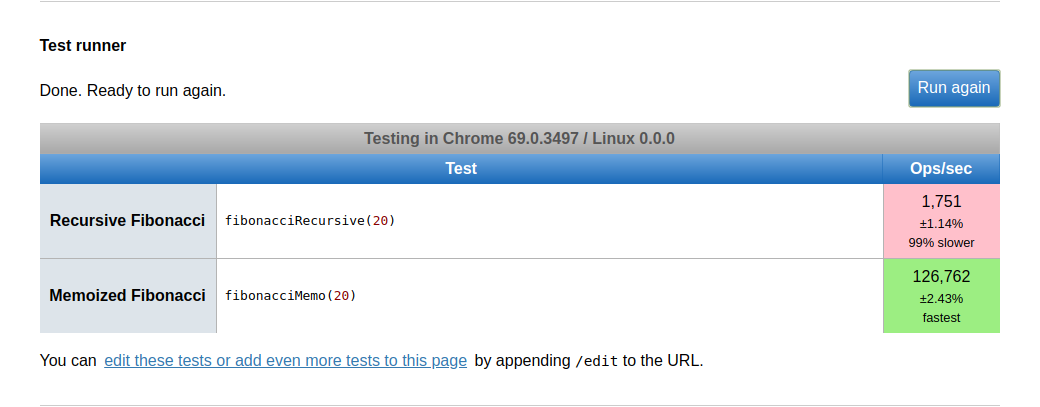
😲 와우 !!! 정말 인상적이네요. 메모화(memoized)된 피보나치 함수는 예상대로 가장 빠릅니다.

매우 놀랍습니다. 1,751 ops/sec로 실행하고 약 99% 느린 순수 재귀 솔루션은 126,762 ops/sec 로 실행합니다.

참고 : "ops / sec"는 초당 작업 수를 나타내며 이는 테스트가 1초에 실행될 것으로 예상되는 횟수입니다.

메모이제이션이 함수(functional) 수준에서 애플리케이션의 성능에 영향을 미칠 수 있는지 살펴 보았습니다. 그렇다면 애플리케이션 내의 모든 비싼 함수에 내부 캐시를 유지하기 위해 수정된 변형을 만들어야 한다는 뜻인가요?

아니요. 함수에서 함수를 반환함으로써 외부에서 실행될 때에도 부모 함수의 범위를 상속하게된다는 사실을 기억하십니까? 이렇게 하면 특정 피처 및 특성(특성)을 둘러싸는 함수에서 반환되는 함수로 전송할 수 있습니다.

우리 자신의 메모이저(memoizer) 함수를 작성하면서 이것을 메모이제이션(memoization에 적용 해 봅시다.

함수형 접근

아래 코드 스니펫에서는 memoizer라는 고차 함수를 만듭니다. 이 함수를 통해 우리는 어떤 함수에든 쉽게 메모이제이션을 적용할 수 있을 것입니다.

function memoizer(fun){
    let cache = {}
    return function (n){
        if (cache[n] != undefined ) {
          return cache[n]
        } else {
          let result = fun(n)
          cache[n] = result
          return result
        }
    }
}

위에서, 우리는 단순히 memoizer라고 불리는 새로운 함수를 만들어 fun 함수를 받아들여 매개변수로 기억합니다. 함수 내에서 나중에 사용할 수 있도록 함수 실행 결과를 저장하기 위한 cache 오브젝트를 생성한다.

memoizer 함수로부터 위에서 설명한 클로저의 원리로 인해 캐시(cache)가 어디서 실행되든 캐시에 접근할 수 있는 새로운 함수를 반환합니다.

반환 된 함수 내에서if..else 문을 사용하여 지정된 key (parameter) n에 대해 이미 캐시 된 값이 있는지 확인합니다.

있다면 반환합니다. 없는 경우에는 fun 으로 메모화 할(memoized) 함수를 사용하여 결과를 계산합니다.

그 후 적절한 키 n을 사용하여 cache 결과(result)를 추가하여 나중에 액세스 할 수 있도록 합니다. 마지막에 계산된 result를 반환합니다.

꽤 부드럽습니다 !

처음에 고려된 재귀 피보나치 함수에 memoizer 함수를 적용하려면 함수를 인수로 전달하는 memoizer 함수를 호출합니다 .

const fibonacciMemoFunction = memoizer(fibonacciRecursive)

memoizer 함수 테스트

memoizer 함수를 위의 샘플 케이스와 비교해보면 다음과 같은 결과가 나옵니다.

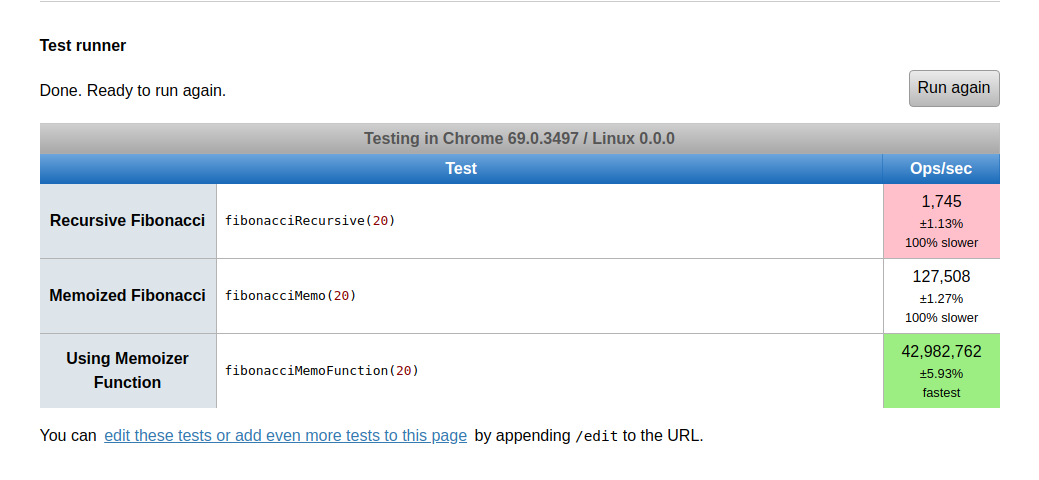
😲 😲 😲 말도 안 돼 !!!! 우리의 메모 함수는 42,982,762 ops/sec로 가장 빠른 솔루션을 생성했습니다. 이전 솔루션은 100% 더 느립니다.

최적화는 어떻습니까!

우리는 이제 무엇을, 왜, 어떻게 를 고려했습니다. 이제 시간을 살펴보겠습니다.

함수를 메모화(memoize) 할 때

물론 메모이제이션은 놀랍고 이제 모든 함수를 메모화(memoize)하고 싶을 수도 있습니다. 그것은 매우 비생산적 일 수 있습니다. 다음은 메모이제이션이 도움이되는 네 가지 경우입니다.

• 비싼 함수 호출, 즉 무거운 계산을 수행하는 함수
• 캐시된 값이 (그저 거기에 앉아) 아무것도 하지 않는 것처럼 제한적이고 매우 반복적 인 입력 범위를 가진 함수의 경우.
• 반복 입력 값이 있는 재귀 함수의 경우.
• 순수한 함수, 즉 특정 입력으로 호출 될 때마다 동일한 출력을 반환하는 함수의 경우.

다 끝냈어! 이제 알겠죠, 그렇죠?

메모이제이션 라이브러리

다음은 메모화 함수를 제공하는 라이브러리입니다.

• Lodash
• Memoizer
• Fastmemoize
• Moize
• Redux를 위해 다시 선택

결론

메모이제이션을 사용하면 함수가 동일한 결과를 반복해서 다시 계산하는 함수를 호출하는 것을 방지 할 수 있습니다. 이제 이 지식을 적용 할 때입니다.

가서 전체 코드베이스를 메모화(memoize) 할 수 있습니다! 😅 (농담)

추가 읽기

이 문서에서 설명하는 기술과 개념에 대해 자세히 알아 보려면 다음 링크를 사용할 수 있습니다.

• Memoization
• 자바 스크립트 클로저 및 스코프 체인의 기본 프로세스 이해
• 고차 함수
• 자바 스크립트에서 메모이제이션 구현

이 아티클처럼요? Twitter에서 @worldclassdev 팔로우